1 5 On A Graph

Systems of Equations and Inequalities

In previous chapters we solved equations with one unknown or variable. We will at present written report methods of solving systems of equations consisting of two equations and two variables.

POINTS ON THE Plane

OBJECTIVES

Upon completing this section you should be able to:

1. Correspond the Cartesian coordinate system and place the origin and axes.
2. Given an ordered pair, locate that bespeak on the Cartesian coordinate system.
3. Given a point on the Cartesian coordinate organization, country the ordered pair associated with it.

Nosotros have already used the number line on which we have represented numbers as points on a line.

Note that this concept contains elements from 2 fields of mathematics, the line from geometry and the numbers from algebra. Rene Descartes (1596-1650) devised a method of relating points on a airplane to algebraic numbers. This scheme is chosen the Cartesian coordinate system (for Descartes) and is sometimes referred to as the rectangular coordinate system.

This system is composed of 2 number lines that are perpendicular at their zero points.

Perpendicular means that two lines are at right angles to each other.

Study the diagram carefully as you note each of the following facts.

The number lines are called axes. The horizontal line is the x-axis and the vertical is the y-axis. The zero point at which they are perpendicular is chosen the origin.

Axes is plural. Axis is atypical.

Positive is to the right and up; negative is to the left and down.

The arrows bespeak the number lines extend indefinitely. Thus the plane extends indefinitely in all directions.

The plane is divided into 4 parts called quadrants. These are numbered in a counterclockwise direction starting at the upper right.

Points on the plane are designated by ordered pairs of numbers written in parentheses with a comma between them, such as (five,seven). This is called an ordered pair because the order in which the numbers are written is of import. The ordered pair (v,7) is not the same as the ordered pair (7,5). Points are located on the plane in the following manner.

Showtime, start at the origin and count left or correct the number of spaces designated by the commencement number of the ordered pair. 2d, from the indicate on the 10-axis given by the starting time number count upwards or downwardly the number of spaces designated by the second number of the ordered pair. Ordered pairs are e'er written with x first and then y, (x,y). The numbers represented by x and y are called the coordinates of the point (x,y).

This is important. The first number of the ordered pair e'er refers to the horizontal management and the second number always refers to the vertical direction.

Example 1 On the post-obit Cartesian coordinate arrangement the points A (3,4), B (0,5), C (-two,7), D (-4,1), E (-3,-4), F (4,-2), G (0,-5), and H (-6,0) are designated. Check each 1 to make up one's mind how they are located.

What are the coordinates of the origin?

GRAPHING LINEAR EQUATIONS

OBJECTIVES

Upon completing this department you should be able to:

1. Find several ordered pairs that make a given linear equation true.
2. Locate these points on the Cartesian coordinate system.
3. Depict a straight line through those points that represent the graph of this equation.

A graph is a pictorial representation of numbered facts. At that place are many types of graphs, such every bit bar graphs, circular graphs, line graphs, and so on. You lot can usually find examples of these graphs in the fiscal section of a newspaper. Graphs are used because a picture show usually makes the number facts more than easily understood.

In this section nosotros will discuss the method of graphing an equation in ii variables. In other words, we will sketch a picture of an equation in ii variables.
Consider the equation x + y - seven and notation that we tin can easily find many solutions. For instance, if 10 = 5 and so y - two, since 5 + 2 = 7. Also, if ten = 3 and so y = 4, since 3 + 4 = 7. If we stand for these answers as ordered pairs (x,y), then we have (5,2) and (3,4) as two points on the airplane that represent answers to the equation x + y = 7.

All possible answers to this equation, located as points on the aeroplane, will give us the graph (or picture) of the equation.

Of form we could never observe all numbers x and y such that x + y = 7, so we must be content with a sketch of the graph. A sketch tin be described as the "curve of best fit." In other words, it is necessary to locate enough points to give a reasonably accurate moving picture of the equation.

Remember, at that place are infinitely many ordered pairs that would satisfy the equation.

Example 1 Sketch the graph of 2x + y = iii.

Solution Nosotros wish to find several pairs of numbers that will brand this equation true. We volition accomplish this by choosing a number for x then finding a corresponding value for y. A table of values is used to record the data.

In the top line (10) we will place numbers that nosotros have chosen for x. Then in the bottom line (y) we volition identify the corresponding value of y derived from the equation.

Of class, we could too kickoff by choosing values for y and and so find the respective values for ten.

In this example we will allow x to accept on the values -three, -2, -1,0, 1,2,3.

These values are capricious. We could choose any values at all.

Find that in one case we have chosen a value for x, the value for y is adamant past using the equation.

These values of 10 give integers for values of y. Thus they are good choices. Suppose we chose

These facts give u.s. the following table of values:

Nosotros now locate the ordered pairs (-3,9), (-2,7), (-one,v), (0,3), (ane,1), (2,-1), (3,-iii) on the coordinate plane and connect them with a line.

We now accept the graph of 2x + y = 3.

The line indicates that all points on the line satisfy the equation, as well as the points from the table. The arrows indicate the line continues indefinitely.

The graphs of all first-degree equations in two variables will be direct lines. This fact volition exist used here fifty-fifty though it will be much later on in mathematics before you can prove this statement. Such start-degree equations are chosen linear equations.

Thus, any equation of the form ax + by - c where a, b, and c are real numbers is a linear equation.

Equations in two unknowns that are of higher caste give graphs that are curves of different kinds. You volition written report these in future algebra courses.

Since the graph of a first-degree equation in two variables is a straight line, it is only necessary to have two points. However, your piece of work will be more consistently accurate if yous notice at to the lowest degree three points. Mistakes tin be located and corrected when the points found do non lie on a line. Nosotros thus refer to the third point as a "checkpoint."

This is important. Don't try to shorten your piece of work past finding simply two points. You volition exist surprised how often you will find an error by locating all three points.

Example 2 Sketch the graph of 3x - 2y - 7.

Solution Starting time make a table of values and determine on three numbers to substitute for x. We will try 0, 1,ii.

Again, you could likewise accept started with arbitrary values of y.

The answer is not as like shooting fish in a barrel to locate on the graph as an integer would be. So information technology seems that x = 0 was not a very good choice. Sometimes it is possible to look ahead and make better choices for x.

Since both x and y are integers, x = 1 was a good choice.

The point (1,-ii) will be easier to locate. If x = two, we will accept another fraction.

The signal (3,1) volition be piece of cake to locate.

x = three was another practiced choice.

We volition readjust the tabular array of values and use the points that gave integers. This may not always be viable, but trying for integral values will give a more accurate sketch. We now accept the tabular array for 3x - 2y = 7.

We can do this since the choices for ten were arbitrary.

Locating the points (one,-ii), (3,1), (- one,-5) gives the graph of 3x - 2y = 7.

How many ordered pairs satisfy this equation?

Slope OF A LINE

OBJECTIVES

Upon completing this section you should be able to:

1. Acquaintance the slope of a line with its steepness.
2. Write the equation of a line in slope-intercept form.
3. Graph a direct line using its slope and y-intercept.

We now wish to hash out an important concept called the gradient of a line. Intuitively we can recollect of slope equally the steepness of the line in human relationship to the horizontal.

Post-obit are graphs of several lines. Written report them closely and mentally answer the questions that follow.

Which line is steeper?

What seems to exist the relationship between the coefficient of 10 and the steepness Which graph would exist steeper: of the line when the equation is of the form y = mx?

Which graph would exist steeper: y = 3x or y = 7x?

Now report the following graphs.

Which line is steeper?

What effect does a negative value for chiliad take on the graph?

Which graph would be steeper: y = 3x or y = 7x?

For the graph of y = mx, the following observations should have been made.

1. If m > 0, and so
   • equally the value of m increases, the steepness of the line increases and
   • the line rises to the correct and falls to the left.
2. If m < 0, then
   • every bit the value of m increases, the steepness of the line decreases and
   • the line rises to the left and falls to the right

Remember, k > 0 means "m is greater than zero."

In other words, in an equation of the form y - mx, m controls the steepness of the line. In mathematics we use the word slope in referring to steepness and class the following definition:

In an equation of the class y = mx, thousand is the gradient of the graph of the equation.

Example 1 Sketch the graph of y = 6x and give the slope of the line.

Solution We get-go make a tabular array showing 3 sets of ordered pairs that satisfy the equation.

Recollect, we simply need 2 points to make up one's mind the line just nosotros utilise the third betoken as a check.

We and then sketch the graph.

The value of grand is 6, therefore the slope is 6. Nosotros may merely write m - half dozen.

Case 2 Sketch the graph and state the gradient of

Solution Choosing values of x that are divisible past iii, we obtain the table

Why use values that are divisible by 3?

Then the graph is

The slope of

Nosotros now wish to compare the graphs of two equations to plant another concept.

Instance 3 Sketch the graphs of y 3x and y - 3x + two on the same set of coordinate axes.

Compare the coefficients of x in these two equations.

Solution

In example three expect at the tables of values and notation that for a given value of ten, the value of y in the equation y = 3x + 2 is 2 more than the corresponding value of y in the equation y = 3x.

Look now at the graphs of the two equations and notation that the graph of y = 3x + 2 seems to have the aforementioned slope equally y = 3x. Also annotation that if the entire graph of y = 3x is moved upward two units, it will be identical with the graph of y = 3x + ii. The graph of y = 3x crosses the y-axis at the point (0,0), while the graph of y = 3x + 2 crosses the y-axis at the signal (0,2).

Once more, compare the coefficients of x in the two equations.

Compare these tables and graphs as in example iii.

Discover that when two lines have the same slope, they are parallel.

The slope from i point on a line to another is adamant by the ratio of the change in y to the change in x. That is,

Note that the modify in ten is 3 and the change in y is two.

The modify in 10 is -4 and the modify in y is 1.

We could also say that the alter in x is 4 and the change in y is - 1. This will outcome in the same line.

Example 7 In the graph of y = 3x - 2 the slope is 3.

The modify in x is i and the modify in y is 3.

y = mx + b is called the slope-intercept form of the equation of a straight line. If an equation is in this form, thou is the slope of the line and (0,b) is the point at which the graph intercepts (crosses) the y-centrality.

The point (0,b) is referred to as the y-intercept.

If the equation of a directly line is in the slope-intercept form, it is possible to sketch its graph without making a table of values. Use the y-intercept and the gradient to draw the graph, as shown in example 8.

Note that this equation is in the grade y = mx + b.

Get-go locate the point (0,-ii). This is one of the points on the line. The slope indicates that the changes in 10 is iv, so from the point (0,-2) we motility four units in the positive direction parallel to the x-axis. Since the change in y is 3, we and then move three units in the positive direction parallel to the y-axis. The resulting indicate is also on the line. Since ii points make up one's mind a directly line, nosotros then describe the graph.

Always commencement from the y-intercept.
A common error that many students brand is to confuse the y-intercept with the ten-intercept (the indicate where the line crosses the ten-axis).

Instance nine Give the slope and y-intercept and sketch the graph of y = 3x + 4.

Solution k = -3, y-intercept = (0,4).

To express the slope as a ratio nosotros may write -iii equally or . If we write the slope as , and then from the point (0,four) we move ane unit of measurement in the positive direction parallel to the x-centrality so move 3 units in the negative direction parallel to the y-axis. Then we draw a line through this point and (0,four).

Suppose an equation is not in the course y = mx + b. Tin nosotros still discover the gradient and y-intercept? The respond to this question is yes. To practice this, however, we must change the form of the given equation by applying the methods used in department 4-2.

Section 4-2 dealt with solving literal equations. Y'all may want to review that section.

Example x Find the slope and y-intercept of 3x + 4y = 12.

Solution First we recognize that the equation is non in the slope-intercept form needed to respond the questions asked. To obtain this form solve the given equation for y.

Example 11 Find the slope and y-intercept of 2x - y = seven.

Solution Placing the equation in gradient-intercept grade, we obtain

Sketch the graph of the line on the grid below.

GRAPHING LINEAR INEQUALITIES

OBJECTIVES

Upon completing this section you should be able to graph linear inequalities.

In chapter 4 nosotros synthetic line graphs of inequalities such as

These were inequalities involving only one variable. We found that in all such cases the graph was some portion of the number line. Since an equation in two variables gives a graph on the plane, it seems reasonable to assume that an inequality in two variables would graph as some portion or region of the plane. This is in fact the case. The solution of the inequality x + y < five is the gear up of all ordered pairs of numbers {x,y) such that their sum is less than 5. (x + y < 5 is a linear inequality since x + y = v is a linear equation.)

Instance 1 Are each of the following pairs of numbers in the solution set of ten + y < 5? (two,i), (three,-four), (5,6), (3,2), (0,0), (-1,4), (-two,8).

Solution

The solution gear up consists of all ordered pairs that make the statement truthful.

To summarize, the following ordered pairs give a true statement.
(ii,1),(3,-4),(0,0),(-1,4)

The post-obit ordered pairs give a faux statement.
(5,vi),(3,two),(-2,viii)

Following is a graph of the line x + y = 5. The points from example i are indicated on the graph with answers to the question "Is x + y < 5?"

Find that all the points that satisfy the equation are to the left and below the line while all the points that will not are to a higher place and to the correct.

Observe that all "yep" answers prevarication on the same side of the line x + y = 5, and all "no" answers prevarication on the other side of the line or on the line itself.

The graph of the line x + y = v divides the plane into iii parts: the line itself and the two sides of the lines (called half-planes).

x + y < 5 is a half-aeroplane
x + y < 5 is a line and a half-plane.

If one point of a half-plane is in the solution set of a linear inequality, then all points in that one-half-airplane are in the solution set. This gives u.s.a. a convenient method for graphing linear inequalities.

To graph a linear inequality
1. Supplant the inequality symbol with an equal sign and graph the resulting line.
ii. Check one point that is obviously in a detail half-airplane of that line to see if it is in the solution fix of the inequality.
3. If the bespeak chosen is in the solution set, and so that entire half-plane is the solution set. If the signal chosen is not in the solution gear up, then the other one-half-plane is the solution set.

Why do we need to check only 1 point?

Example 2 Sketch the graph of 2x 4- 3y > vii.

Solution Footstep i: First sketch the graph of the line 2x + 3y = vii using a table of values or the slope-intercept form.

Step two: Next cull a betoken that is not on the line 2x + 3y = seven. [If the line does not become through the origin, and then the signal (0,0) is always a good choice.] Now plow to the inequality 2x + 3y> > 7 to see if the chosen point is in the solution gear up.

Footstep three: The signal (0,0) is non in the solution set, therefore the one-half-plane containing (0,0) is not the solution set. Hence, the other halfplane determined past the line 2x + 3y = 7 is the solution gear up.
Since the line itself is not a role of the solution, information technology is shown as a dashed line and the half-airplane is shaded to evidence the solution fix.

The solution set is the half-plane above and to the right of the line.

Case 3 Graph the solution for the linear inequality 2x - y ≥ 4.

Solution Footstep i: First graph 2x - y = 4. Since the line graph for 2x - y = 4 does not go through the origin (0,0), cheque that point in the linear inequality.

Step 2:

Step 3: Since the point (0,0) is not in the solution set, the half-plane containing (0,0) is not in the set. Hence, the solution is the other half-plane. Notice, notwithstanding, that the line 2x - y = 4 is included in the solution set. Therefore, draw a solid line to show that it is function of the graph.

The solution set is the line and the one-half-aeroplane beneath and to the right of the line.

Instance 4 Graph ten < y.

Solution Starting time graph x = y. Next cheque a indicate not on the line. Notice that the graph of the line contains the point (0,0), so nosotros cannot use it as a checkpoint. To decide which half-plane is the solution fix use any point that is apparently not on the line x = y. The betoken ( - 2,three) is such a point.

Using this information, graph x < y.

When the graph of the line goes through the origin, any other betoken on the x- or y-axis would likewise exist a good selection.

GRAPHICAL SOLUTION OF A SYSTEM OF LINEAR EQUATIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Sketch the graphs of two linear equations on the same coordinate system.
2. Make up one's mind the common solution of the two graphs.

Example 1 The pair of equations is chosen a system of linear equations.

We have observed that each of these equations has infinitely many solutions and each will class a straight line when we graph it on the Cartesian coordinate system.

Nosotros now wish to detect solutions to the system. In other words, we desire all points (x,y) that will exist on the graph of both equations.

Solution We reason in this manner: If all solutions of 2x - y = two lie on ane straight line and all solutions of x + 2y = 11 lie on another straight line, and so a solution to both equations will be their points of intersection (if the two lines intersect).

In this tabular array we permit ten take on the values 0, 1, and two. We then find the values for y by using the equation. Practice this before going on.
In this tabular array nosotros let y take on the values two, 3, and half-dozen. We and so detect x by using the equation. Bank check these values also.

The two lines intersect at the signal (iii,4).

Annotation that the point of intersection appears to exist (3,4). Nosotros must now check the point (3,4) in both equations to see that it is a solution to the system.

As a check we substitute the ordered pair (3,4) in each equation to come across if we get a truthful statement.
Are at that place any other points that would satisfy both equations? Why?

Therefore, (iii,4) is a solution to the organisation.

Not all pairs of equations will requite a unique solution, as in this example. At that place are, in fact, iii possibilities and you should be aware of them.

Since nosotros are dealing with equations that graph as straight lines, we can examine these possibilities past observing graphs.

ane. Contained equations The 2 lines intersect in a single betoken. In this instance there is a unique solution.

The example higher up was a system of independent equations.

2. Inconsistent equations The ii lines are parallel. In this case there is no solution.

No thing how far these lines are extended, they will never intersect.

3. Dependent equations The two equations requite the same line. In this example any solution of one equation is a solution of the other.

In this case there will exist infinitely many common solutions.

In later algebra courses, methods of recognizing inconsistent and dependent equations will be learned. However, at this level we volition deal only with independent equations. You can and then look that all bug given in this chapter volition accept unique solutions.

This means the graphs of all systems in this chapter will intersect in a unmarried point.

To solve a arrangement of two linear equations by graphing
i. Make a table of values and sketch the graph of each equation on the same coordinate system.
ii. Discover the values of (x,y) that name the indicate of intersection of the lines.
3. Check this bespeak (x,y) in both equations.

Once more, in this tabular array wc arbitrarily selected the values of x to be - ii, 0, and 5.
Here nosotros selected values for 10 to be 2, 4, and half dozen. You could have chosen any values you wanted.
Nosotros say "apparent" because we have not still checked the ordered pair in both equations. One time it checks it is then definitely the solution.

Since (3,two) checks in both equations, it is the solution to the organisation.

GRAPHICAL SOLUTION OF A System OF LINEAR INEQUALITIES

OBJECTIVES

Upon completing this department yous should exist able to:

1. Graph ii or more than linear inequalities on the same set of coordinate axes.
2. Determine the region of the plane that is the solution of the system.

After studies in mathematics will include the topic of linear programming. Fifty-fifty though the topic itself is across the scope of this text, i technique used in linear programming is well within your attain-the graphing of systems of linear inequalities-and we will discuss information technology here.

Y'all found in the previous section that the solution to a system of linear equations is the intersection of the solutions to each of the equations. In the same manner the solution to a system of linear inequalities is the intersection of the half-planes (and perhaps lines) that are solutions to each individual linear inequality.

In other words, ten + y > 5 has a solution set and 2x - y < 4 has a solution fix. Therefore, the system

has equally its solution set the region of the aeroplane that is in the solution fix of both inequalities.

To graph the solution to this organization we graph each linear inequality on the same set of coordinate axes and signal the intersection of the two solution sets.

Note that the solution to a system of linear inequalities will exist a drove of points.

Again, utilize either a tabular array of values or the gradient-intercept grade of the equation to graph the lines.

Checking the point (0,0) in the inequality 10 + y > five indicates that the signal (0,0) is not in its solution fix. We indicate the solution set of x + y > 5 with a screen to the right of the dashed line.

This region is to the right and above the line 10 + y = 5.

Checking the point (0,0) in the inequality 2x - y < 4 indicates that the point (0,0) is in its solution set. We signal this solution set with a screen to the left of the dashed line.

This region is to the left and to a higher place the line 2x - y = 4.

The intersection of the two solution sets is that region of the plane in which the 2 screens intersect. This region is shown in the graph.

Note once again that the solution does not include the lines. If, for example, we were asked to graph the solution of the system

which indicates the solution includes points on the line x+ y = 5.

The results indicate that all points in the shaded section of the graph would be in the solution sets of ten + y > v and 2x - y < iv at the aforementioned time.

SOLVING A SYSTEM BY Substitution

OBJECTIVES

Upon completing this section y'all should exist able to solve a system of two linear equations by the substitution method.

In section 6-5 we solved a system of two equations with ii unknowns by graphing. The graphical method is very useful, but it would non be practical if the solutions were fractions. The actual point of intersection could exist very difficult to decide.
There are algebraic methods of solving systems. In this department we will talk over the method of commutation.

Example one Solve by the substitution method:

Solution
Pace 1 We must solve for one unknown in i equation. We can choose either 10 or y in either the outset or 2nd equation. Our choice can be based on obtaining the simplest expression. In this case we will solve for x in the second equation, obtaining 10 = iv + 2y, because any other selection would have resulted in a fraction.

Look at both equations and see if either of them has a variable with a coefficient of ane.

Footstep ii Substitute the value of x into the other equation. In this case the equation is
2x + 3y = 1.
Substituting (4 + 2y) for ten, we obtain two(four + 2y) + 3y = 1, an equation with only ane unknown.

The reason for this is that if x = four + 2y in i of the equations, then 10 must equal 4 + 2y in the other equation.

Step three Solve for the unknown.

Remember, beginning remove parentheses.

Step 4 Substitute y = - one into either equation to observe the corresponding value for x. Since nosotros have already solved the second equation for 10 in terms of y, we may use it.

We may substitute y = - one in either equation since y has the same value in both.

Thus, nosotros have the solution (2,-1).

Retrieve, ten is written starting time in the ordered pair.

Step five Bank check the solution in both equations. Call back that the solution for a organisation must be truthful for each equation in the system. Since

the solution (2,-1) does check.

This checks: 2x + 3y = i and ten - 2y = 4.

Check this ordered pair in both equations.
Neither of these equations had a variable with a coefficient of one. In this case, solving by commutation is non the best method, simply we will do it that way just to show information technology tin can exist done. The next section volition give the states an easier method.

SOLVING A SYSTEM OF LINEAR EQUATIONS Past ADDITION

OBJECTIVES

Upon completing this section you should be able to solve a arrangement of ii linear equations by the addition method.

The improver method for solving a organization of linear equations is based on two facts that nosotros accept used previously.

First we know that the solutions to an equation practice non modify if every term of that equation is multiplied by a nonzero number. Second we know that if we add the same or equal quantities to both sides of an equation, the results are still equal.

Example i Solve past addition:

Annotation that we could solve this system past the substitution method, by solving the first equation for y. Solve this system by the substitution method and compare your solution with that obtained in this section.

Solution
Pace i Our purpose is to add the two equations and eliminate one of the unknowns so that we tin can solve the resulting equation in one unknown. If we add the equations as they are, we will non eliminate an unknown. This ways we must first multiply each side of one or both of the equations by a number or numbers that will lead to the elimination of one of the unknowns when the equations are added.
Later on carefully looking at the problem, nosotros annotation that the easiest unknown to eliminate is y. This is done by beginning multiplying each side of the get-go equation by -two.

Note that each term must be multiplied by ( - ii).

Step 2 Add together the equations.

Step 3 Solve the resulting equation.

In this instance we simply multiply each side by (-1).

Step 4 Find the value of the other unknown by substituting this value into one of the original equations. Using the kickoff equation,

Substitute x = four in the second equation and see if you get the same value for y.

Step 5 If we cheque the ordered pair (iv,-3) in both equations, nosotros see that information technology is a solution of the system.

Example 2 Solve past improver:

Note that in this system no variable has a coefficient of one. Therefore, the best method of solving it is the improver method.

Solution
Step ane Both equations will have to be changed to eliminate one of the unknowns. Neither unknown will be easier than the other, so cull to eliminate either 10 or y.
To eliminate x multiply each side of the first equation by iii and each side of the second equation by -2.

If you choose to eliminate y, multiply the first equation by - 2 and the second equation past 3. Do this and solve the system. Compare your solution with the one obtained in the example.

Footstep 2 Calculation the equations, we obtain

Footstep 3 Solving for y yields

Step 4 Using the first equation in the original system to discover the value of the other unknown gives

Step 5 Bank check to run into that the ordered pair ( - one,3) is a solution of the system.

The cheque is left up to y'all.

STANDARD FORM

OBJECTIVES

Upon completing this department you should be able to:

1. Write a linear equation in standard form.
2. Solve a organisation of 2 linear equations if they are given in nonstandard course.

Equations in the preceding sections have all had no fractions, both unknowns on the left of the equation, and unknowns in the aforementioned order.
Such equations are said to exist in standard form. That is, they are in the class ax + by = c, where a, b and c are integers. Equations must exist inverse to the standard grade before solving by the addition method.

Instance 1 Alter 3x = five + 4y to standard grade.

Solution 3x = 5 + 4y is non in standard class because one unknown is on the correct. If we add -4y to both sides, nosotros have 3x - 4y = 5, which is in standard course.

Be careful here. Many students forget to multiply the right side of the equation by 24.

Again, make certain each term is multiplied by 12.

Now add - 24x to both sides, giving - 24x + 9y = -10, which is in standard form. Usually, equations are written then the first term is positive. Thus we multiply each term of this equation past (- 1).

Instead of maxim "the first term is positive," nosotros sometimes say "the leading coefficient is positive."

WORD PROBLEMS WITH Two UNKNOWNS

OBJECTIVES

Upon completing this section you lot should be able to:

1. Determine when a give-and-take problem can exist solved using two unknowns.
2. Determine the equations and solve the give-and-take problem.

Many word problems can be outlined and worked more easily past using two unknowns.

Example i The sum of ii numbers is 5. Iii times the commencement number added to five times the second number is 9. Find the numbers.

Solution Allow x = first number
y = 2nd number
The first statement gives the states the equation
ten + y = five.
The 2d statement gives us the equation
3x + five y = 9.
Nosotros now take the system

which we can solve by either method we have learned, to give
ten = 8 and y = - iii.

Solve the system by exchange.

Example two Two workers receive a total of $136 for viii hours work. If i worker is paid $1.00 per hr more than than the other, detect the hourly rate for each.

Solution Let 10 = hourly charge per unit of i worker
y = hourly rate of other worker.

Notation that information technology is very important to say what ten and y represent.

The commencement statement gives united states the equation
8x + 8y = 136.
The second statement gives the equation
x = y + 1.
We now accept the system (in standard grade)

Solving gives x = ix and y = 8. I worker's rate is $ix.00 per hour and the other'southward is $8.00 per hour.

Solve this system by the improver method.

SUMMARY

Key Words

• The Cartesian coordinate organization is a method of naming points on a aeroplane.
• Ordered pairs of numbers are used to designate points on a airplane.
• A linear equation graphs a straight line.
• The slope from one point on a line to some other is the ratio .
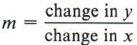• The slope-intercept form of the equation of a line is y = mx + b.
• A linear inequality graphs as a portion of the aeroplane.
• A system of 2 linear equations consists of linear equations for which we wish to find a simultaneous solution.
• Independent equations take unique solutions.
• Inconsistent equations take no solution.
• Dependent equations have infinitely many solutions.
• A system of 2 linear inequalities consists of linear inequalities for which nosotros wish to discover a simultaneous solution.
• The standard course of a linear equation is ax + past = c, where a, b, and c are real numbers.

Procedures

• To sketch the graph of a linear equation find ordered pairs of numbers that are solutions to the equation. Locate these points on the Cartesian coordinate organization and connect them with a line.
• To sketch the graph of a line using its slope:
  Step one Write the equation of the line in the class y - mx + b.
  Step two Locate the j-intercept (0,b).
  Step 3 Starting at (0,b), use the slope m to locate a second bespeak.
  Step 4 Connect the two points with a directly line.
• To graph a linear inequality:
  Step ane Replace the inequality symbol with an equal sign and graph the resulting line.
  Stride ii Bank check one point that is evidently in a detail one-half-aeroplane of that line to see if it is in the solution gear up of the inequality.
  Step 3 If the point called is in the solution set, and then that entire half-aeroplane is the solution set. If the indicate chosen is not in the solution prepare, then the other halfplane is the solution set.
• To solve a arrangement of two linear equations by graphing, graph the equations carefully on the aforementioned coordinate organisation. Their point of intersection volition exist the solution of the system.
• To solve a system of 2 linear inequalities by graphing, make up one's mind the region of the plane that satisfies both inequality statements.
• To solve a system of two equations with two unknowns by substitution, solve for one unknown of one equation in terms of the other unknown and substitute this quantity into the other equation. Then substitute the numerical value thus found into either equation to detect the value of the other unknown. Finally, check the solution in both equations.
• To solve a arrangement of two equations with two unknowns by add-on, multiply 1 or both equations by the necessary numbers such that when the equations are added together, i of the unknowns will exist eliminated. Solve for the remaining unknown and substitute this value into one of the equations to discover the other unknown. Cheque in both equations.
• To solve a give-and-take trouble with two unknowns find 2 equations that bear witness a human relationship between the unknowns. And so solve the organisation. E'er check the solution in the stated problem.

1 5 On A Graph,

Source: https://quickmath.com/webMathematica3/quickmath/graphs/inequalities/basic.jsp

Posted by: carrolloakedy.blogspot.com

Share this post